|
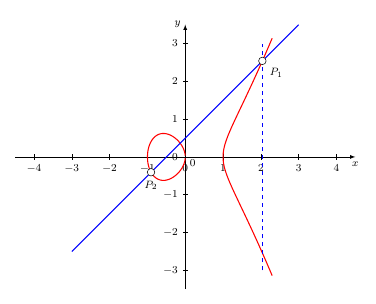
Ich habe Funktionen mit TikZ gezeichnet, die sich schneiden. In den Schnittpunkten möchte ich jeweils einen dicken Punkt setzten, damit man diese besser erkennt. Neben den Schnittpunkt soll dann direkt etwas stehen. \documentclass[margin=5mm, tikz]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usepackage{amsmath, amssymb} \begin{document} \begin{tikzpicture}[ x=1cm, y=1cm, scale=1.0, font=\footnotesize, >=latex ] \draw[->] (-4.5,0) -- (4.5,0) node[below] {$x$}; \foreach \x in {-4,...,4} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {\footnotesize $\x$}; \draw[->] (0,-3.5) -- (0,3.5) node[left] {$y$}; \foreach \y in {-3,...,3} \draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {\footnotesize $\y$}; \draw[color=black] (0pt,-5pt) node[right] {\footnotesize $0$}; \draw[thick,color=red] plot[samples=200, domain=1:2.3] (\x,{sqrt((\x^3-\x))}) node[] {}; \draw[thick,color=red] plot[samples=200, domain=1:2.3] (\x,{-sqrt((\x^3-\x))}) node[] {}; \draw[thick,color=red] plot[samples=200, domain=0:-1] (\x,{sqrt((\x^3-\x))}) node[] {}; \draw[thick,color=red] plot[samples=200, domain=0:-1] (\x,{-sqrt((\x^3-\x))}) node[] {}; \draw[thick, color=blue] plot[samples=200, domain=-3:3] (\x,{\x+0.5}) node[] {}; \draw[thick, color=blue, dashed] (2.039, -3) -- (2.039,3); \end{tikzpicture} \end{document} |
|
Eine Möglichkeit wäre das von Hand zu machen: %.... %Schnittpunkt \draw [red, fill=yellow] (2.039,2.539) circle (2pt) node[right] {$S$}; \end{tikzpicture} Rest wie gehabt. Eine Lösung mit der Bibliothek 'intersections' bekomme ich für diese Kurven im Moment nicht hin. Habe es nun so gelöst.
(15 Apr '14, 14:49)
lalaland
|
|
Eine Lösung mit automatischer Bestimmung der Schnittpunkte:
Relevante Ausschnitte hierfür: \usetikzlibrary{intersections} \tikzset{schnittpunkt/.style={circle, inner sep = 2pt, draw, fill = white}} ... \draw[name path=funktion4, thick,color=red] plot[samples=200, domain=-1:0] (\x,{-sqrt((\x^3-\x))}) node[] {}; \draw[name path=linie, thick, color=blue] plot[samples=200, domain=-3:3] (\x,{\x+0.5}) node[] {}; \path[name intersections={of=linie and funktion4}] node at (intersection-1) [schnittpunkt,label=below:{$P_2$}] {}; Gesamtes Codebeispiel: \documentclass[margin=5mm, tikz]{standalone} \usepackage[ngerman]{babel} \usepackage{tikz} \usetikzlibrary{intersections} \tikzset{schnittpunkt/.style={circle, inner sep = 2pt, draw, fill=white}} \usepackage{amsmath, amssymb} \begin{document} \begin{tikzpicture}[ x=1cm, y=1cm, scale=1.0, font=\footnotesize, >=latex ] \draw[->] (-4.5,0) -- (4.5,0) node[below] {$x$}; \foreach \x in {-4,...,4} \draw[shift={(\x,0)},color=black] (0pt,2pt) -- (0pt,-2pt) node[below] {\footnotesize $\x$}; \draw[->] (0,-3.5) -- (0,3.5) node[left] {$y$}; \foreach \y in {-3,...,3} \draw[shift={(0,\y)},color=black] (2pt,0pt) -- (-2pt,0pt) node[left] {\footnotesize $\y$}; \draw[color=black] (0pt,-5pt) node[right] {\footnotesize $0$}; \draw[name path=funktion1, thick,color=red] plot[samples=200, domain=1:2.3] (\x,{sqrt((\x^3-\x))}) node[] {}; \draw[name path=funktion2, thick,color=red] plot[samples=200, domain=1:2.3] (\x,{-sqrt((\x^3-\x))}) node[] {}; \draw[name path=funktion3, thick,color=red] plot[samples=200, domain=-1:0] (\x,{sqrt((\x^3-\x))}) node[] {}; \draw[name path=funktion4, thick,color=red] plot[samples=200, domain=-1:0] (\x,{-sqrt((\x^3-\x))}) node[] {}; \draw[name path=linie, thick, color=blue] plot[samples=200, domain=-3:3] (\x,{\x+0.5}) node[] {}; \draw[thick, color=blue, dashed] (2.039, -3) -- (2.039,3); \path[name intersections={of=linie and funktion1}] node at (intersection-1) [schnittpunkt,label=below right:{$P_1$}] {}; \path[name intersections={of=linie and funktion4}] node at (intersection-1) [schnittpunkt,label=below:{$P_2$}] {}; \end{tikzpicture} \end{document}
Den anderen Schnittpunkt, analog Schnitt von Das Prinzip habe ich verstanden. Hätte aeigentlich gedacht, dass der dritte Schnittpunkt durch den Schnittpunkt von "funktion4" und "linie" ebenfalls angezeigt wird...
(15 Apr '14, 14:49)
lalaland
@Stefan Den Schnittpunkt mit
(15 Apr '14, 16:40)
esdd
|
|
Hier ist noch ein Vorschlag, bei dem alle Schnittpunkte von TikZ ermittelt werden. Falls die gestrichelte Linie eine Senkrechte zur x-Achse durch den Schnittpunkt sein soll, dann kann man auch diese einzeichnen lassen, ohne den Punkt zu berechnen. \documentclass[margin=5mm, tikz]{standalone} \usepackage{tikz} \usetikzlibrary{intersections} \begin{document} \begin{tikzpicture}[ font=\footnotesize, >=latex, kurve/.style={thick,red,samples=100,domain=#1}, gerade/.style={thick,blue,samples=2,domain=#1}, punkt/.style={circle,inner sep=2pt,fill=white,draw}, ] %Koordinatensystem \draw[->] (-4.5,0) -- (4.5,0) node[below] {$x$}; \foreach \i in {1,...,4}{\foreach \x in {-\i,\i} \draw[shift={(\x,0)}] (0pt,2pt) -- (0pt,-2pt) node[below] {$\x$};} \draw[->] (0,-3.5) -- (0,3.5) node[left] {$y$}; \foreach \i in {1,...,3}{\foreach\y in {-\i,\i} \draw[shift={(0,\y)}] (2pt,0pt) -- (-2pt,0pt) node[left] {$\y$};} \node[below left] {$0$}; %Kurve \foreach[count=\i] \d/\v in {1:2.3/,1:2.3/-,0:-1/,0:-1/-} \draw[kurve=\d,name path=k\i]plot(\x,{\v sqrt((\x^3-\x))}); %Beseitigen der Lücke bei x=-1 \foreach \v in {,-} \draw[thick,red,samples at={-1,-.99}]plot(\x,{\v sqrt((\x^3-\x))}); %Gerade \draw[gerade=-3:3,name path=g] plot(\x,{\x+0.5}); %%% ---- %Schnittpunkte ermitteln und beschriften \foreach[count=\i] \m/\o in {1/right,3/right,4/below} \node[name intersections={of={k\m} and g,name=s\i},label=\o:$S_\i$]at(s\i-1){}; %gestrichelte Senkrechte durch 1.Schnittpunkt \draw[thick,blue,dashed](s1-1|- 0,-3)--(s1-1|-0,3); %Schnittpunkte einzeichnen \foreach\i in {1,2,3}\node[punkt]at(s\i-1){}; \end{tikzpicture} \end{document} Außerdem kann man auch noch den zweiten Schnittpunkt der gestrichelten Linie mit der Kurve einzeichnen lassen. Dazu ist es notwendig, die gestrichelte Linie mittels \documentclass[margin=5mm]{standalone} \usepackage{tikz} \usetikzlibrary{intersections} \begin{document} \begin{tikzpicture}[ font=\footnotesize, >=latex, kurve/.style={thick,red,samples=100,domain=#1}, gerade/.style={thick,blue,samples=2,domain=#1}, punkt/.style={circle,inner sep=2pt,fill=white,draw}, ] %Koordinatensystem \draw[->] (-4.5,0) -- (4.5,0) node[below] {$x$}; \foreach \i in {1,...,4}{\foreach \x in {-\i,\i} \draw[shift={(\x,0)}] (0pt,2pt) -- (0pt,-2pt) node[below] {$\x$};} \draw[->] (0,-3.5) -- (0,3.5) node[left] {$y$}; \foreach \i in {1,...,3}{\foreach \y in {-\i,\i} \draw[shift={(0,\y)}] (2pt,0pt) -- (-2pt,0pt) node[left] {$\y$};} \node[below left] {$0$}; %Kurve \foreach[count=\i] \d/\v in {1:2.3/,1:2.3/-,0:-1/,0:-1/-} \draw[kurve=\d,name path=k\i]plot(\x,{\v sqrt((\x^3-\x))}); %Beseitigen der Lücke bei x=-1: \foreach \v in {,-} \draw[thick,red,samples at={-1,-.999,...,-.99}]plot(\x,{\v sqrt((\x^3-\x))}); %Gerade \draw[gerade=-3:3,name path=g] plot(\x,{\x+0.5}); %%% ---- %Schnittpunkte ermitteln und beschriften \foreach[count=\i] \m/\o in {1/right,3/right,4/below} \node[name intersections={of={k\m} and g,name=s\i},label=\o:$S_\i$]at(s\i-1){}; %gestrichelte Senkrechte durch 1.Schnittpunkt \draw[thick,blue,dashed,name path=gestrichelt](s1-1|- 0,-3)--(s1-1|-0,3); %Schnittpunkte einzeichnen \foreach\i in {1,2,3}\node[punkt]at(s\i-1){}; %%% ---- %weiterer Schnittpunkt gestrichelte Linie \node[name intersections={of=gestrichelt and k2}, label=right:Extrapunkt,punkt,fill=yellow]at(intersection-1){}; \end{tikzpicture} \end{document} Ziemlich krass zusammengefaßt. Den letzten Schnittpunkt unten rechts, falls man den auch noch braucht, muß man dann vermutlich manuell ermitteln lassen.
(15 Apr '14, 16:52)
cis
@cis Meinst du den zweiten mit der gestrichelten Linie? Den könnte man auch einzeichnen lassen.
(15 Apr '14, 16:55)
esdd
Ja genau, den einzigen unmarkierten. Das könntest Du als Beispiel für eine intersection ohne Schleifen usw. dazuschreiben.
(15 Apr '14, 17:19)
cis
|