|
Hi, ich bin ganz neu hier und hoffe, ihr könnt mir helfen. Ich möchte folgendes Gitter mit dem
Bild von Wikipedia (Creative Commons Attribution-Share Alike 3.0 Unported) Ich habe versucht das Gitter durch linerare Funktionen darzustellen, aber es gibt bestimmt bessere Wege. Das Gitter ist bei meiner Methode vor der x- und y-Achse, sollte aber besser dahinter liegen. Ich weiß nicht wie das geht :( gibt es ne elegante Methode? Danke!! |
|
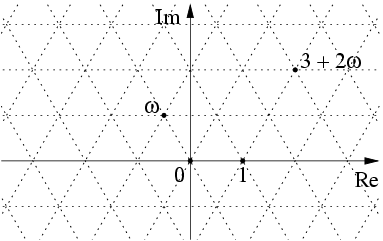
Ich mag TikZ! \documentclass[tikz]{standalone} \begin{document} \begin{tikzpicture}[dot/.style={draw,fill,circle,inner sep=1pt}] \draw[->] (-3,0) -- (4,0) node[below] {$\mathop{\mathrm{Re}}$}; \draw[->] (0,-1) -- (0,4) node[left] {$\mathop{\mathrm{Im}}$}; \begin{scope} \clip (-3,-1) rectangle (4,4); \foreach \i in {-5,-4,...,5} { \draw[dotted] (\i,0) +(-120:2) -- +(60:6); } \foreach \i in {-5,-4,...,5} { \draw[dotted] (\i,0) +(-60:2) -- +(120:6); } \foreach \i in {-2,-1,...,4} { \draw[dotted] (-4,{\i/2*sqrt(3)}) -- (4,{\i/2*sqrt(3)}); } \end{scope} \node[dot,label={below left:$0$}] at (0,0) {}; \node[dot,label={below:$1$}] at (1,0) {}; \node[dot,label={above left:$\omega$}] at (-.5,{1/2*sqrt(3)}) {}; \node[dot,label={above right:$3 + 2\omega$}] at (2,{sqrt(3)}) {}; \end{tikzpicture} \end{document} |
|
Hier ist noch ein Vorschlag mit TikZ, bei dem das Gitter in einem Makro definiert wird und deshalb mehrmals verwendet werden kann. Das Gitter selbst wird aus kleinen gitter/.pic={\draw(1,0)--++(120:2)--+(1,0)--(0,0)(0,0|-60:1)--+(1,0);} Ein einzelnes
Diese Gitterelemente werden in einer Schleife eingefügt, so dass sie den gesamten Hintergrund des Koordinatensystems füllen. Bei jeder Verwendung eines Für das Eintragen der Punkte habe ich die Idee mit der Koordinatentransformation aus der Antwort von @Clemens übernommen, so dass sie hier ebenfalls einfach mit (x,omega) angegeben werden können. \documentclass[tikz,margin=5mm]{standalone} \usetikzlibrary{calc} \tikzset{ dot/.style={draw,fill,circle,inner sep=1pt},% Stil für Punkte gitter/.style={dotted},% Stil für das Gitter % Gitterelement als pic: gitter/.pic={\draw(1,0)--++(120:2)--+(1,0)--(0,0)(0,0|-60:1)--+(1,0);} } \newcommand\Dreiecksgitter[5][]{% % Größe des gezeigten Bereichs: \def\xmin{#2}\def\ymin{#3} \def\xmax{#4}\def\ymax{#5} % Gitter einfügen \begin{scope} % Gitterbereich beschneiden (lokal, da in scope): \clip (\xmin,\ymin) rectangle (\xmax,\ymax); % ganzzahlige Grenzen für die Schleife (lokal, da in scope) \pgfmathsetmacro\xmin{floor(\xmin)};\pgfmathsetmacro\ymin{floor(\ymin/(sqrt(3))}; \pgfmathsetmacro\xmax{ceil(\xmax)};\pgfmathsetmacro\ymax{ceil(\ymax/sqrt(3))}; % Einfügen der Gitterelement in Schleife \pic foreach \x in {\xmin,...,\xmax} foreach \y in {\ymin,...,\ymax} [gitter,#1] at (\x,{\y*sqrt(3)}){gitter}; \end{scope} % % Achsen und Ursprung einzeichnen \draw[-latex] (\xmin,0) -- (\xmax,0) node[below left,inner xsep=0pt] {Re}; \draw[-latex] (0,\ymin) -- (0,\ymax) node[below left,inner ysep=0pt] {Im}; } \begin{document} \begin{tikzpicture} % Gitter mit Achsen einfügen \Dreiecksgitter[blue]{-3.6}{-1}{3.6}{3} % Eintragen der Punkte mit Koordinatentransformation \begin{scope}[ cm={1,0,-0.5,{sqrt(3)/2},(0,0)}, % Koordinatentransformation every node/.style={dot} ] \node[label={below left:$0$}] at (0,0) {}; \node[label={below:$1$}] at (1,0) {}; \node[label={above left:$\omega$}] at (0,1) {}; \node[label={above right:$3 + 2\omega$}] at (3,2) {}; \node[label={above right:$-2 - \omega$}] at (-2,-1) {}; \end{scope} \end{tikzpicture} \begin{tikzpicture} % Gitter mit Achsen einfügen \Dreiecksgitter[red]{-3.6}{-3}{8.6}{10.2} \end{tikzpicture} \end{document} |
|
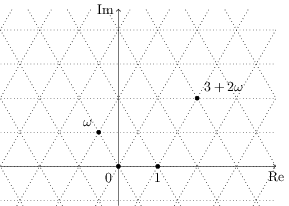
Eine Idee wäre, ein entprechendes Koordinatensystem (cs) zu verwenden. Dann könnte man mit \begin{tikzpicture}[ cm={1,0,-.5,.5*sqrt(3),(0,0)} , % Koordinatentransformation dot/.style={draw,fill,circle,inner sep=1pt} , % Darstellung der Punkte gridlines/.style={dotted} % Gitterstil ] % Größe des gezeigten Bereichs: \def\xmin{-3.6}\def\xmax{3.6} \def\ymin{-1.3}\def\ymax{3.3} % Gitter: \draw[gridlines] (\xmin,\ymin) grid (\xmax,\ymax) ; \end{tikzpicture}
Damit ein rechteckiger Ausschnitt entsteht, schneide ich mit \begin{tikzpicture}[ cm={1,0,-.5,.5*sqrt(3),(0,0)} , % Koordinatentransformation dot/.style={draw,fill,circle,inner sep=1pt} , % Darstellung der Punkte gridlines/.style={dotted} % Gitterstil ] % Größe des gezeigten Bereichs: \def\xmin{-3.6}\def\xmax{3.6} \def\ymin{-1.3}\def\ymax{3.3} % überstehender Bereich des Gitters, damit keine Lücken enstehen: \def\deltagrid{5} % Berechnung des gezeichneten Bereichs: \pgfmathsetmacro\xgridmin{round(\xmin-\deltagrid)} \pgfmathsetmacro\xgridmax{round(\xmax+\deltagrid)} \pgfmathsetmacro\ygridmin{round(\ymin-\deltagrid)} \pgfmathsetmacro\ygridmax{round(\ymax+\deltagrid)} % clip Rechteck mit Original-cs: \clip[reset cm] (\xmin,\ymin) rectangle (\xmax,\ymax) ; % Gitter: \draw[gridlines] (\xgridmin,\ygridmin) grid (\xgridmax,\ygridmax) ; \end{tikzpicture}
Jetzt fehlen noch ein paar Linien. Die können mit einer for-Schleife gezeichnet werden, bei der ich eine weitere Transformation des cs vornehme. (Achtung: es ist eine Transformation des aktuellen, schon transformierten cs). \foreach \x in {\xgridmin,...,\xgridmax} { \show\x \draw[gridlines,cm={1,0,1,1,(0,0)}] (\x,\ygridmin) -- (\x,\ygridmax) ; }
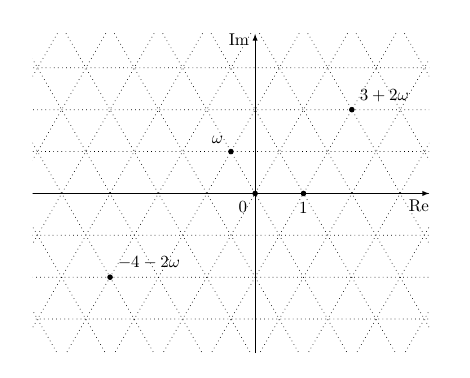
Jetzt fehlen noch die Achsen (im ursprünglichen cs) und die Punkte. Die Punkte können jetzt einfach mit (x,omega) angegeben werden. \documentclass{article} \usepackage{tikz} \begin{document} \begin{tikzpicture}[ cm={1,0,-.5,.5*sqrt(3),(0,0)} , % Koordinatentransformation dot/.style={draw,fill,circle,inner sep=1pt} , % Darstellung der Punkte gridlines/.style={dotted} % Gitterstil ] % Größe des gezeigten Bereichs: \def\xmin{-4.6}\def\xmax{3.6} \def\ymin{-3.3}\def\ymax{3.3} % überstehender Bereich des Gitters, damit keine Lücken enstehen: \def\deltagrid{5} % Berechnung des gezeichneten Bereichs: \pgfmathsetmacro\xgridmin{round(\xmin-\deltagrid)} \pgfmathsetmacro\xgridmax{round(\xmax+\deltagrid)} \pgfmathsetmacro\ygridmin{round(\ymin-\deltagrid)} \pgfmathsetmacro\ygridmax{round(\ymax+\deltagrid)} % clip Rechteck mit Original-cs: \clip[reset cm] (\xmin,\ymin) rectangle (\xmax,\ymax) ; % Gitter: \draw[gridlines] (\xgridmin,\ygridmin) grid (\xgridmax,\ygridmax) ; \foreach \x in {\xgridmin,...,\xgridmax} { \show\x \draw[gridlines,cm={1,0,1,1,(0,0)}] (\x,\ygridmin) -- (\x,\ygridmax) ; } % Achsen im Original-cs: \draw[-latex] (\xmin,0) -- (\xmax,0) node[below left,inner xsep=0pt] {Re} ; \draw[-latex,reset cm] (0,\ymin) -- (0,\ymax) node[below left,inner ysep=0pt] {Im}; % Punkte im neuen cs: \node[dot,label={below left:$0$}] at (0,0) {}; \node[dot,label={below:$1$}] at (1,0) {}; \node[dot,label={above left:$\omega$}] at (0,1) {}; \node[dot,label={above right:$3 + 2\omega$}] at (3,2) {}; \node[dot,label={above right:$-4 - 2\omega$}] at (-4,-2) {}; \end{tikzpicture} \end{document}
|




Willkommen auf der TeXwelt :)
Es ist immer eine gute Idee zu zeigen, was man selbst bisher gemacht hat. Bitte füge ein Minimalbeispiel von Deinen bisherigen Versuchen ein und nimm uns etwas Arbeit ab das ganze selbst aufzusetzen.