|
Ich hätte eine Frage. Sofern die Umsetzung dieser Frage zu kompliziert ist bzw. zu viel Aufwand wäre dann ist es auch egal. Keine hohe Priorität wäre nur Nice to Have. Ich nehme "mein" Beispiel zur Hand. \documentclass[11pt,tikz]{standalone} \usepackage[T1]{fontenc} \usepackage[scaled]{uarial} \renewcommand*\familydefault{\sfdefault} \begin{document} \begin{tikzpicture} \draw[fill opacity=0.7, fill=gray,gray](-3.7,-1.06)--(3.7,-1.06)--(3.7,3.7)--(-3.7,3.7)--(-3.7,-1.06); \fill[black](-0.56,0.56)--(-0.56,1.352)--(-1.352,0.56)--(-0.56,0.56); \fill[black](0.56,0.56)--(0.56,1.352)--(1.352,0.56)--(0.56,0.56); \draw[dash pattern=on 5.5mm off 2mm on .5mm off 2mm, -,line width=1pt](0,0)--(-3.2,0); \draw[dash pattern=on 5.5mm off 2mm on .5mm off 2mm, -,line width=2pt](0,0)--(0,3.2); \draw[dash pattern=on 5.5mm off 2mm on .5mm off 2mm, -,line width=2pt](0,0)--(3.2,0); \draw[red,line width=3pt](0,-0.56)--(-3.2,-0.56); \draw[fill=red] (0,0) circle [radius=0.2cm]; \draw(0,-0.56)--(0,0.56); \draw(0,0.56)--(-3.2,0.56); \draw(-0.56,0)--(-0.56,3.2); \draw(-0.56,0)--(0.56,0); \draw(0.56,0)--(0.56,3.2); \draw(0,0.56)--(3.2,0.56); \draw(0,0.56)--(0,-0.56); \draw(0,-0.56)--(3.2,-0.56); \fill[red](-1.592,0.56)circle (0.06); \draw[red](-1.592,0.56)--(-1.592,0.96); \node[above left,rotate=0,red] at (-1.592,0.96){$0$}; \fill[red](-0.56,1.592)circle (0.06); \draw[red](-0.56,1.592)--(-0.96,1.592); \node[above left,rotate=0,red] at (-0.96,1.592){$1$}; \fill[red](0.56,1.592)circle (0.06); \draw[red](0.56,1.592)--(0.96,1.592); \node[above right,rotate=0,red] at (0.96,1.592){$2$}; \fill[red](1.592,0.56)circle (0.06); \draw[red](1.592,0.56)--(1.592,0.96); \node[above right,rotate=0,red] at (1.592,0.96){$3$}; \draw[->,blue,line width=2pt]( 0,0)--(-2.22,0)node[above]{$y$}; \draw[->,blue,line width=2pt]( 0,0)--(0,2.22)node[left]{$z$}; \end{tikzpicture} \end{document} Diese Zeichnung spielt sich im 2 Dimensionalen Raum ab. (x/y). Könnte ich diese Zeichnung irgendwie eine z- Ausdehnung geben? Sodass ich ein Volumen erhalte? Einfach die Zeichnung um ein gewissen Betrag nach hinten zu schieben ausgehend vom Ursprung. Momentan sehe ich nur die Aufsicht. (Die Sicht von Vorne). Angenommen ich drehe den Betrachtungswinkel um einen gewissen Bereich nach Links oder Rechts dann würde ich das Objekt schräg sehen. Ich würde ein 3D Objekt sehen sofern ich vorher die Verschiebung gemacht habe... Dh: Ich würde ein wenig von Vorne sehen und die Seitenansicht. Ich hoffe ihr versteht meine Frage. Danke für eure Antwort bzw. sonst ein schönes Wochenende. |
|
Dein "Minibsp." mir etwas zu sehr BruteForce-Coded, als das ich das schnell überall durchsteigen kann. Tipp: Versuche möglichst zu konstruieren; am besten mit relativen Positionsangaben, als mit absoluten Koordinaten. Ich vermute, Du willst irgendwie sowas:
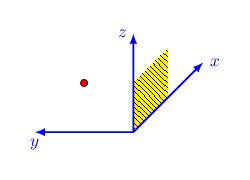
\documentclass[margin=5mm, tikz]{standalone} \usepackage[T1]{fontenc} %\usepackage[scaled]{uarial} \usepackage[ngerman]{babel} \renewcommand*\familydefault{\sfdefault} \usepackage{tikz} \usetikzlibrary{patterns} \begin{document} \begin{tikzpicture}[ x={({cos(45)},{sin(45)})}, y={(-1cm,0cm)}, z={(0cm,1cm)}, >=latex, ] \draw[fill=red] (0,1,1) circle[radius=2pt]; \fill[yellow, postaction={pattern=north west lines}] (0,0,0) -- (1,0,0) -- (1,0,1) -- (0,0,1) -- cycle; % KoSy \tikzstyle{KoSy}[1pt]=[->,draw=blue,line width=#1] \draw[KoSy](0,0,0)--(2,0,0)node[right]{$x$}; \draw[KoSy](0,0,0)--(0,2,0)node[below]{$y$}; \draw[KoSy](0,0,0)--(0,0,2)node[left]{$z$}; \end{document} @cis mir fehlt ein wenig der Durchblick bei der richtigen Koordinaten-Eingabe von: begin{tikzpicture}[ x={({cos(45)},{sin(45)})}, y={(-1cm,0cm)}, z={(0cm,1cm)},
Das Bild wird dann verzerrt dargestellt. Ich hätte aber gerne so ein Standbild (unverzerrt) wie man bei folgender Lösung sieht: http://texwelt.de/wissen/fragen/13328/drehung-einer-tikz-zeichnung-im-raum-um-eine-achse/13339
(28 Sep '15, 11:33)
basel
|

Gibt es keine Lösung? :/
So:
\draw[->,blue,line width=2pt]( 0,0)--(2.22,2.22,0)node[left]{$x$};oder wie? Und alles andere entsprechend...das hast du dovh im Prinzip schon mal gefragt: http://texwelt.de/wissen/fragen/13328/drehung-einer-tikz-zeichnung-im-raum-um-eine-achse/13339